OK... so today we reviewed a few old concepts and started on some new ones.
FIRST things first...
That, my friends, is the "normal" bell curve. The curve pretty much everything everywhere falls into. But what does it show us exactly?
Lets take a peek at how its devided up...
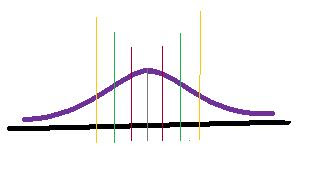
OK... so between the red lines lies 68% of all data.
between the Green lines lies 95% of all data.
between the Yellow Lines lies 99.7% of all data.
Now what these sections show us is not JUST the % of data within each sections.
Between any two z-scores chosen along the axis of the curve we can find the are, the percentage AND a probability all in one.
On another point, remeber how befor we had to worry about window settings and clearing pictures ans so on jsut to find the ara between two z-scores? Well frett no more. Mr.K showed us the quick-fast way to do it. Get your calculators ready...
STEPS :
-ON
-2nd
-VARS
-2
You will then on your home screen see somthing that looks like "normalcdf( ". At this point, you type in your z-scores (lowest,highest) OR your range, mean then the standard deviation.. in that order , seperated by commas... like so (low end of the range,high end of the range, mean, standard deviation).
-Don't forget to CLOSE the bracket! )
Quick example of the FIRST way using the Z-scores.
Ex 1. Q. Given the Z scores -.2 and 1.4, what percentage of the data lies in that particular range?
A. normalcdf(-.2,1.4)
*hit enter*
The number you get is 0.4985
That number gives you three things.
-The area between those two numbers is .4985
-The percent of data within those two numbers (49.85%)
-The probability that of all the data collected, that something would be "picked" out of that specific section.
What the question asked for was percentage... so your answer would be 49.85%
Next example of the OTHER way by using the range, mean and standard deviation.
Ex 2. Q. A selection of numbers has been aquired. Given a high of 190 and a low of 160, a mean of 150 and a standard deviation of 10, what is the probability that a selected number from a particular group of numbers is within that range?
A. normalcdf(160,190,150,10)
*hit enter*
You get 0.1586
Final thing we used was the Reverse norm function. It is a function we have that allows us to find the z score using the area.
STEPS:
-ON
-2nd
-VARS
-3
At this point you enter in the area/persentage/prabability.
Well that about summs it up. Gnight.
Next scribe is Eugene.
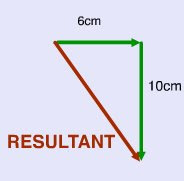
 Using pythagorean theorem as used in the example above, we find the length of the resultant vector as 5 cm.
Using pythagorean theorem as used in the example above, we find the length of the resultant vector as 5 cm.



















 The experiment was done by flipping 4 coins (20 times). Each trial represented one family of four. The probabily for each outcome (0,1,2,3 girls...) was divided by 20 which is the total number of times the experiment was done for.
The experiment was done by flipping 4 coins (20 times). Each trial represented one family of four. The probabily for each outcome (0,1,2,3 girls...) was divided by 20 which is the total number of times the experiment was done for.






