Sorry about the lateness

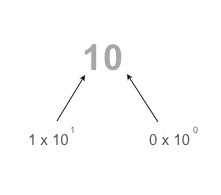
The first thing we learned yesterday was an easier way to find z scores.

1. Go to stat then edit.

2. Then go to L1 and push in the list of numbers.

3. Go to L2 and at the top push in (L1-mean)/the standard deviation.

4. Now you have your z scores :)



We also learnt about Normal distribution





Above is a picture of normal distribution. Notice how it has a bell shape, this will help you indentify normal distribution in a graph. Most of the data in normal distribution is continuous (has decimal places). There are certain properties of normal distribution which are...
1. 68% of data lies within 1 standard deviation of the mean.
2. 95% of data lies within 2 standadrd deviations of the mean.
3. 99.7% of data lies within 3 standard deviation of the mean.

There are other facts about normal distribution. The area under the curve equals one. The x axis is an asymptote for the curve (the line goes close but never hits zero). Tha graph is symetrical. as well the farther away you go out the less data there is.

Another thing we talked about in class is how to find the mean with the z score. To do this you have to follow the formula (z score * standard devation)+ mean



Next is Daniel

Today's Slides: March 27

Here they are ...

Applied 40S March 27, 2009

View more presentations from dkuropatwa.

Niwatori's Corner (Statistics - Zscores!)

KONICHIWA MINA!

Welcome back to Niwatori-san's corner and today is Z-scores. Feed the need for more MATH!

For Your Information. . . . Red Anecdotes Stuff to know/IMPORTANT STUFF but take it however you will
Blue Anecdotes kinda important so like review it if you like
Green is for formulas/calculations with the calculator and so forth


After the briefing of when a standard deviation is 1,2,3 or even 4 deviations above or below the mean... might as well tell you what "above/below standard deviations from the mean" means.

**In short, you have the mean of a set of data and then a standard deviation from the data the whole basis is when you are "below" the mean you subtract the number of standard deviations from the mean getting a negative number. Being "above the mean" just means to add the number of standard deviations to the mean.
The formula for this is: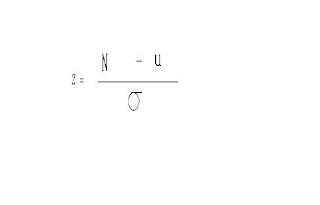When you need to get a Z-score to determine which side is greater than the other you get the Z-scores of all the needed info. Then you compare with which number is greater.

Sorry but I couldn't think of an example right at the moment but look over the slides MR.Kuros posted up.

Look look the thing is for now is to use this formula for the distribution tables and follow along with the lessons to come.

Sorry that this post is short but that's all I can think of with my Knowledge for now.
(Plus it's just a review of what we did anyways so meh sue me >-<)


Anywho.. . . . David-san is the next Scriber! (>_<>

"Eagerness brings the most out of Enthusiasm!"

Niwatori's Corner (Statistics - Looking for patterns)

O hayao gozaimasu mina! (forgot what this means it means "Hello everyone in formal context =p)

!!!!For Ya Imfomation. . . . . . !!!!!!
Blue anecdotes sorta inportant
Red anecdotes Stuff to check/IMPORTANT STUFF take it however you will
Green is for formulas/any calculator stuff!



Anywho. . . today I will serve you with both the Looking for patterns in Statistics "Grouped data" as well as how to get these Z-scores but keep yourself tuned for the next posting for the Z-scores part =p


Yes, well just to quote Mr.Kuros and his masterful words of math ( = [ apparently flattery doesn't get free marks) "Math is the Science of Patterns" it really is. You are looking for simliar patterns and then apply them to what we are given to us. Basically saying, having things you know and utilize the ideas/patterns to solve something new unknown to us.

Ok? Ok! >_<

Remember hearing about the difference between "S" and "O" Standard Deviations?
Well here's the thing "S" is for a sample of a large data in which for the learning process of Statistics we're only using "o" in this case the sign "SIGMA" anecdotes for "sum of" to find the neccessary info which is the population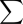

an example is a survey of favorite car around the world where 1000 people out of 40000 people in the country take the survey and then taking that info to predict everyone elses choice of car. This is considered the "S" type being that this is a large piece of data.

"o" type for example is the survey given to Sisler High School and then seeing who likes which car. A small population such as a local school is considered "o" type where data is small.
Ok now?

Now on with Niwatori-san's Diagrams
--follow them and ask for questions like comments/or at school ask for some help you all know who Niwatori-san is =P--

-See now we were taught the day before of something called a "Frequency distribution table"
as well as a "Probability distribution table" actually the probablity one is just the figures/numbers in percentages! So these diagrams will review my knowledge of how to crack at this shell in a nutshell! -





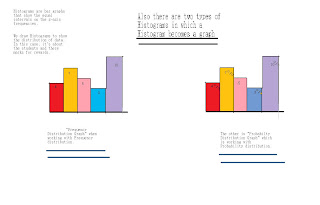
The above diagram shows a Histogram and this bar graph will be your friend.

To build one go to (STAT PLOT) on the (Y=) button but press the (2nd) button 1st from that press the 1st one for now. After this Highlight and press the ON side. The x-value will always be L1, the frequency will be different depending if your working with a probability/frenquency graph. --HINT-- L3 for probability most of the time L2 for the frequency most of the time trust me you`ll understand when you press them!


Well that concludes this portion. Wait till morning for the next page. I needed to rest sorry folks.

Anyways the next scriber is David-san!

*Passes baton skoots away pwoosh pwoosh pwoosh*

"My hope is today is tommorrow`s colorful"
-By Niwatori-san-

Today's Slides: March 25

Here they are ...

Applied 40S March 25, 2009

View more presentations from dkuropatwa.

Today's Slides: March 24

Here they are ...

Applied 40S March 24, 2009

View more presentations from dkuropatwa.

MAN AM I TIRED.

Alright childrens, here's some things you should consider.

IMPORTANT CONCEPTS

1. When grouping, it is important to understand that patterns are more important than details. For example, if you had two tons of fruits, all different kinds, and half of your fruits were rotten... You want to group those and get rid of them. Whether or not it's an apple or an orange can wait, honestly!

2. When measuring how extreme a particular piece of data is, find it's distance from the mean in standard deviations! For example, If there are twenty cars on the road, and the mean speed of the cars is 50 mph with a standard deviation of two mph... Well, let's just say that if one of those cars is flying down the road at 60 mph, that'd be a little extreme! *note: 50-60 with standard deviation of 2 is a 5x(standard deviation) difference! Five standard deviations, in relation to road speed, is too dang fast!

3. REMEMBER! There are two ways to find Standard Deviation! There's a sample version and a population version. The most pronounced difference is that to find the Standard Deviation of a sample, you divide by n-1 instead of n! 

Well. Those are a few concepts we should consider for next class. I'd go into more detail, but I'd rather wait until I have a firmer grasp of this unit, I wouldn't want to sabotage any of you folks.

THE NEXT SCRIBE WILL BE PHONG, BECAUSE HE CAN SAVE US ALL.

Today's Slides: March 23

Here they are ...

Applied 40S March 23, 2009

View more presentations from dkuropatwa.

Introduction to Statistics

Today in class we started our Statistics unit. We started the class going over some ideas (found on the first couple slides) to start thinking about why and how statistics is used. Then we got into vocabulary. The terms are important and can be found on the 6th slide. There are also other notes following this and we also have a few homework questions. Mr. K stressed that this unit can be difficult and it is IMPORTANT to stop him and ask questions as soon as something is unclear. We spent a lot of time on Measures of Central Tendency and Dispersion today.

Measures of Central Tendency: Mean, Median, and Mode:

Mean: The mean can be found by adding up all of the quantities given and dividing that sum by the number of quantities that were added. The equation for calculating the mean is:
Where "x bar" represents the mean,
"N" represents the total number of quantities (if you added five numbers together this N would equal 5,
X means the sum of all data
For ex. If you had the numbers 17 11 23 6 and 3.
To find the mean add up all the numbers:

17+11+23+6+3=60.
Next divide the sum (60) by the number of quantities that were added.
60/5
The answer would be: 12

Median: The median is the middle number in a given set of numbers. If the total number of numbers is even then the median is found by adding the two middle numbers and dividing by two. For example. If you had the numbers 17 11 23 6 and 3
The median would be found by first sorting the numbers from smallest to biggest
3 6 11 17 23
Next you would find the number in the middle:
11 If the set of numbers was 3 6 11 17 23 and 30
You would need to take the two middle numbers and add them then divide by two.
(11+17)/2
The answer would be 14.

Mode: The mode is the number that occurs most often in a set of data. When there are two numbers that show up an equal number of times it is termed Bimodal Distribution. *NOTE: When used in class distribution refers to "a bunch of data".
For example: If you had the numbers 8 14 14 20 and 24
The mean would be 14.
If the numbers were 8 14 14 20 20 24
The answer would be 14 and 24
Click here for practice problems

Measures of Dispersion: Range and Standard Deviation:

Range: The range is the difference between the smallest and largest values in a data set. The only values that matter when calculating the range are the highest and lowest numbers!
For example if you had the numbers: 5 10 15 20 and 25
Locate your highest number: 25
lowest number: 5
And subtract: 20
Standard Deviation: In standard deviation all the numbers in a data set 'matter'. It is a measure that shows how the data is dispersed in reference to the mean.
The symbol for Standard Deviation is

Calculator:
Mr. K also went over in class how to use our calculators for some of the calculations we will be learning this unit.

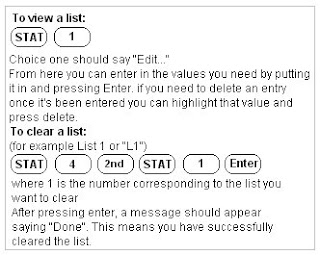
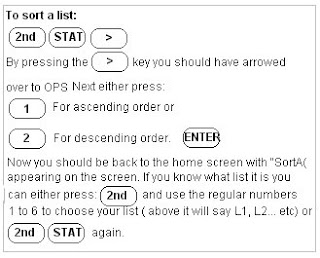
Next Scribe is Daniel

Today's Slides: March 20

Here they are ...

Applied 40S March 20, 2009

View more presentations from dkuropatwa.

Today during class we did our "Pre-test" for our current unit of probability. The pre-test prepares us for our upcomming unit test which takes place tomorrow March 19. The format of our pre-test was 2 multiple choice questions, 2 short answer questions, and 1 3-step problem. We were given about 35-40 minutes to write our pre-test and after that Mr. K split us up into groups to compare answers. After about ten minutes of comparing answers, Mr. K went over the questions and showed us step by step how it came out to the answer.


In my group there were a couple a questions that stumpted my group members and I, but now I understand why and how we got the answer.

Here is one question that we didn't quite get right..

Using the word FOOD, find the probability that an arrangement of this word will begin with the two O's if all the letters are used. Correct to the nearest hundreth.

So to start off, you need to make sure that the two O's are stuck together at the front of the four letter combination. A way that Mr. K would refer it to would be "take the two O's and put them in a bag."


And this is what the 4 letter word combination can look like..




The first 1 stands for the 2 O's which are "stuck together," they are first because the question requires for them to be at the front of the four letter combination. The 2 stands for the choice of either F or D. And the last 1 stands for the left over of the previous two. (Say I choose F for the second space, then the last space would be a D and vice versa.)

So now you are required to multiply 1 by 2 by 1 in order to find out the number of ways for the combination. The answer is 2.

Now you take the the amount of ways that the four letter word can be rearranged(2 differnt ways) and you divide it by 4 factorial(representing the total number of letters) divided by 2 factorial(representing the 2 O's)

You would do it like so..



The result would be 2/12 then would reduce into 1/6, and because the question says around to the nearest hundreth, you must express the faction into a decimal which is 0.17.



* JUST A REMINDER * our unit test is tomorrow!
For further review Mr. K posted up extra questions.

I choose Kayla for the next scribe!

Today's Slides: March 18

Here they are ...

Applied 40S March 18, 2009

View more presentations from dkuropatwa.

Hi everybody, just a heads up there is a pre-test tomorrow so be prepared.

Any who today in class we learned two new topics. These topics are called Mutually exclusive and Non Mutually exclusive events. The way something can be mutually exclusive is if it is impossible for them to occur together. Basically like saying you can't be the age 31 and at the same time be 16, there is just no way. Or like saying can you roll a die and get both a positive and negative number at the same time.

Examples

Drawing one card either, a black ace or a red two

When randomly selecting two animals from a barn either a, cat or dog

Randomly selecting a person either a, girl or a boy

Now non mutually exclusive events are the exact opposites when things can happen together, like either drawing from a deck of cards a king or a spade. You can actually draw a king of spades.

Examples

Selecting a person for your basketball team who is either, fast or tall

Sleeping with either a, long pillow or comfy pillow

Rolling a two dice and either getting a sum of an odd number or a double

Although you may just think of this as the exact opposite to mutually exclusive events there is more thinking involved. Mutually exclusive event formula is (A) n (B) = zero set, done. For non mutually exclusive events there is a big formula you have to follow.

Using Mr.K's example I will explain

You wish to draw either a king or a spade from a single deck
A represents kings
B represents spades
Now remember one card is both keep this in mind

So the formula looks like this P ( A U B ) = P(A) + P(B) - P(AnB)
Plug in the numbers and you it looks like
P ( A U B ) = 4/52 + 13/52 - 1/52
= 1/16

WHOA, why did we subtract the 1/52 people may ask, reason being because the card gets counted so we want to subtracted it so that it doesn't get counted twice.

So that is what we learned in class what I recommend doing is try to make up your own mutually and non mutually exclusive events and practise further with the formula. Now the next scribe I choose is IRIS......

Today's Slides: March 17

Here they are ...

Applied 40S March 17, 2009

View more presentations from dkuropatwa.

Today's Slides: March 16

Here they are ...

Applied 40S March 16, 2009

View more presentations from dkuropatwa.

Today in class Mr. K started off by putting us into groups. We were then given problems to solve. You can check the slide for today.



Independent and Dependent event

My understanding about Dependent Variable it's called dependent variable because it's distribution of values depends upon the distribution of the other values or in other words It is something that depends on other factors while Independent Variable is a variable whose value determines the value of other variables or it is a variable that stands alone and isn't changed by other variable.


Here are some examples

The Probability of heads landing up when you flip a coin is 1/2

What is the probability of getting tails if you flip it again? It is still 1/2
The two events do not affect each other because it is an Independent event.

click to open the box

Two balls are drawn successively without replacement from a box which contains 4 blue balls and 3 red balls.
Find the probability that:

(a) the first ball drawn is blue and the second is red
(b) both balls are red.

The second event is dependent on the first

P(blue) = 4/7

There are 6 balls left and out of those 6, three of them are red. So the probability that the second one is red is given by:

P(red) = 3/6 = 1/2 reminder always simplify

dependent event so 4/7 × 1/2 = 2/7

Also dependent event. Using same method, but realizing there will be 2 red balls on the second draw, we have:



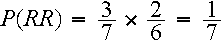
The next scriber I choose is : HENSON

Today's Slides: March 13

Here they are ...

Applied 40S March 13, 2009

View more presentations from dkuropatwa.

Happy Pi Day!

Wishing you the best of Pi Days!!!

Did you know that the U.S. House of Representatives even passed a resolution calling for March 14 to be recognized as "National Pi Day in the United States? You can read about it here.


Photo Credit

Today in class Mr.K started off by putting us into groups. We went over the homework that was assigned to us the night before. The answers to the questions are posted on todays slides, March 12th.


The new lesson we learned today was COMBINATIONS ( the "choose" formula). The formula is as follows:





"n" is the number of objects availabl to be arranged

"r" is the number of objects tht are being arranged




EXAMPLES:















You would read this as 10 "choose" 5 equals 10 divided by 5 factorial multiplied by 5 factorial.


By choosing 5 people to make a team which equals 5!, that means there is remainder of 5 other people from the 10.



The answer to this question is : 252

Another example:

This you would read as 15 "choose" 3 equals 15 divided by 3 factorial multiplied by 12 factorial.

This shows that you would choose 3 people(3!) out of the 15 people (15!) given which leaves you with 12 people (12!) left.

The answer is: 455

Tomorrow is Pi day. So don't forget to bring your pies. Also remember to find a cool math joke to share with the class.

The scriber I choose is:

MAC

Today's Slides: March 12

Here they are ...

Applied 40S March 12, 2009

View more presentations from dkuropatwa.

Today in class we started off being broken down into groups. We then quickly checked our homework. We were then given a problem to solve, it's on the slides today March 11, slide 9.

The question was:
Suppose that, when you go home from school, you like to take as great a variety of routes as possible, and that you are equally likely to take any possible route. You will walk only east or south.

We used the Pascal's Triangle to solve how many ways we can get from School to home. The answer was 180 ways to get from School to Home.

This is how it was done:














Then we went into more depth of the question, Daniel went up and explained that there was really only a certain way to go home AND pass the post office. This is what he means. The red lines shows how many ways you can pass the post office, from school to home. The blue just shows the extra routes going from school to home, WITHOUT passing through the post office.
















So now getting back to the question which was, what is the probability of passing the post office on your way home.

The answer would be:

Number of ways from School to Home passing the post office: 72
Over the total number of ways from School to Home: 180


SO: 72 / 180 would be the probability of passing through the post office on your way home!

Reminder, always reduce fractions if possible!
Reduced fraction = 2 / 5

And the next scribe would be..

DON !

Today's Slides: March 11

Here they are ...

Applied 40S March 11, 2009

View more presentations from dkuropatwa.

Today's Slides: March 10

Here they are ...

Applied 40S March 10, 2009

View more presentations from dkuropatwa.

Hello There !

Today Mr. K started off with putting us in groups and went over what we did yesterday. He talked and went over the permutations (the 'Pick' formula) examples and the homework that he assigned yesterday. The homework from yesterday took most of the time in class, he also added questions to our homework from yesterday.

The question is: What is the probability that one of these numbers is even if the digits are randomly chosen?, that question goes with question number two part c. We can solve the question by finding the solution of question 2a and 2b and dividing them together to find the probability of one of those numbers to be even when the digits are randomly chosen.

After he went over the homework we had to work on new questions that deals with.....

PERMUTATIONS of NON DISTINGUISHABLE OBJECT. It's the number of ways to arrange n objects that contain K1,K2,K3 set of non distinguishable objects.

Examples:

Book

Since there are 4 letters and 2 letters that are the same the equation would be 4!/2! = 12

Mississippi

Since there are 11 letters and 4S's, 4I's, 2P's, the equation would be 11!/(4!*4!*2!) = 34650.

Non distinguishable object is an easier way of solving problems. We didnt really get to look into it a lot so Mr. K said we would do some more tomorrow !

The next scriber would be....
KYLE ! =)

Today we started off with talking about PI DAY. We get to party this Friday & eat PIE! Not only are we going to eat pie but we get to share math jokes. So everyone don't forget to bring pie along with a stupid math joke.

Our lesson for today was Permutations (the 'Pick' Formula). A permutation is an ordered arrangement of objects.
n - # of objects available to be arranged
r - # of objects that are being arranged

Factorial notation is really an easier way of multiplying all the natural numbers from a particular number down to 1.

We went over our homework as well which are posted on the blog.

Kathrine already knows she's the next scriber.

Today's Slides: March 9

Here they are ...

Applied 40S March 9, 2009

View more presentations from dkuropatwa. (tags: am40sw09 probability)

Counting

Hello everyone! For today's class we started off with Mr. K teaching us how to count in bases. 

First off, we started off with learning how to count with base ten. 

We had the numbers : 0 1 2 3 4 5 6 7 8 9  to work with.  

What he showed us was that from a 10, you start off from the right going to the left. To make this more clear I'll show you all. 

From here we started off with the zero. What we know is that ten to the power of zero is equaled to 1 from there we take the zero and multiply it to ten to the power of zero. 

That there we find out that we would have one-zero. 

Then we would move on to the left, to the one and you would do the exact same thing. 

So now instead of doing ten to the power of zero, we would have ten to the power of one. 

Ten to the power of one would equal to 10. So you have one-ten.  

Here is another example to try to make this more clearer. 

Say I put down 1 2 3 5. 

Then you would have 5 "ones"

3 "tens"

2 "hundreds"

1 "thousand"

Each of these steps is a multiplied by ten. Showing you that it is a base ten. But the one that we will use most would be base two. 

x2^4 = 16     x2^3=8     x2^2=4     x2^1=2     x2^0=1     

That's what I believe we ended with for counting bases. 

Then we moved on to the fundamental principle of counting. 

We first went over our homework that was assigned to us. 

We were taught about factorial. 

Ex. 

8*7*6*5*4*3*2*1 = 40 320

Instead of going doing all that work, he also showed us how to do it on the calculator. 

What you have to do is punch in 8. 

Once you see the number 8 on your screen, you press the button MATH. 

In there you press your arrow key to the left and that would take you to probability. 

When you are there, you would see a exclamation mark. "!" That's what you want to press. 

Hit enter and it would lead you to the main screen. If you hit enter again, it would give you the answer. 

8! = 40 320

What we also found out is that when you do 0!

Then it would equal to one. 

0! = 1 Has been assigned as a DEFINITION. 

When given a question like that, do not write it like so:

10! = 10*9*8*7*6*5*4*3*2*1 = 3 628 800

This is not the proper way to show it. 

After all of the homework review, we also did a group work. 

First question was, How many 4 digit numbers are there in which all the digits are different. 

_  _  _  _ 

Well what I did was that I figured that there are ten numbers, but since you can't use 0 as the first number of the digits, then you would have 9 numbers that you are able to use.  So there are 9 possible numbers that you can use for the first digit. 

9  _  _  _ 

For the second digit slot, you can now use the 0. So you have another 9 options that you are able to put in the second slot because you already used a number in the first slot and you are not able to use it again. So it would look like this:

9  9  _  _

Then for the next one it would be an 8 because you have used another number that is not able to be used again, and so on. 

Then it would be :

9  9  8  7

What you would do with these numbers is you would multiply them together. 

9 * 9 * 8 * 7

That would give us 4536 different ways to put four different digit numbers together. 

The next question is: How many of these digits are odd?

_  _  _  _

What you have to do is figure what odd numbers are there. It would be 1, 3, 5, 7, and 9. There are five odd numbers, so what you would have to do is place a five at the end of the digits like so: 

_  _  _  5

Now that you know how many odd numbers, then you can figure out how many numbers can go into the first digit. Since you used 1 odd number and you can not use a 0 in the first digit, then you only have 8 possibilities of any of the other numbers being in the first digit.

8  _  _  5

For the second digit, you can now use the 0 so the number of possibilities would be 8 again. 

After that the numbers cannot be used again, so the third digit has 7 possibilities. Then it would be : 

8  8  7  5 

Now you multiply them together and you get 2240 possibilities. 

That is what I basically remembered from today's class. 

It's the weekend so have fun! 

But don't forget to also DO YOUR HOMEWORK! 

Next scribe will be ... CAMILLA! =)